一、截位直除法（重点）

截位直除法是一种估算方法，结果可能不是完全精确的，但在很多情况下已经足够接近真实值，可以满足快速计算的需求。

1. 1、截位方法‌：从左往右保留前几位数字（从第一个非零的数字开始），然后对下一位进行四舍五入。例如，对于数字587245，截2位则为59，截3位则为587。

2. 2、截谁：

   1. （1）一步除法（只计算1次除法）：只对分母进行截位。
   2. （2）多步除法（计算多次除法）：分子和分母都需要截位。

3. 3、截几位：

   （1）选项差距大：截两位。 选项首位各不相同，或选项首位相同但次位差大于首位。
   （2）选项差距小：截三位。 选项首位相同，且次位差小于或等于首位。

4. 4、注意：若选项之间存在10、100倍的关系时，要注意判断数量级

INFO

例: 2016年3月全国钢材出口量998万吨，环比增长23.06%，同比增长29.46%。1—3月累计出口钢材2783万吨，累计同比增长7.9%。3月份进口钢材127万吨，环比增长36.56%，同比增长45.08%；1—3月累计进口钢材313万吨，累计同比下降3.3%。 问：2015年3月份进口钢材约为多少万吨？

A.61.3 B.73.5 C.87.5 D.101.3

解析

本题考查基期量计算问题。“2016年3月份进口钢材127万吨，同比增长45.08%”。选项首位不同，分母从左向右截取前两位，代入数据可得，2015年3月份进口钢材约为$\frac{127}{1+45.8}\approx \frac{127}{1.5}$（万吨），直除首位商8。因此，选择C选项。

二、“21”“12”分段法（三位数相减）

1. 1、“21”“12”分段法：将三位数的减法分成“21” 或 “12” 两段，即分成两个两位数或一位数的减法，尽可能保证不用借位。
2. 2、应用：三位数-三位数
3. 3、解释：
   1. （1）“21 分段”：把被减数和减数化成 百位十位 | 个位 的形式，百位十位单独计算，个位单独计算。例如：849-495，可以分成 84-49=35 为第一段，9-5=4 为第二段；849-495=354
   2. （2）“12 分段”：把被减数和减数化成 百位 | 十位个位 的形式，百位单独计算，十位个位单独计算。例如：632-427，可以分成 6-4=2 为第一段，32-27=5 为第二段；632-427=205

INFO

例: 519 - 127

解析

我们发现 个位：9>7；百位＋十位：51>12；使用“21 分段法”，个位=9-7=2；百位＋十位=510-120=390，将数据回归原位，答案=390+2=392。

INFO

例: 572 - 127

解析

我们发现 个位：2<7；十位+个位：72>27；使用“12 分段法”，百位=500-100=400；十位+个位=72-27=45，将数据回归原位，答案=400+45=445。

INFO

例: 513 - 219

解析

使用“12 分段法”，百位=500-200=300；十位+个位=13-19=-6，答案=300-6=294。
使用“21 分段法”，百位＋十位=510-210=300；个位=3-9=-6，答案=300-6=294。

三、拆分法

拆分法就是将一个复杂的问题分解成几个小部分，然后逐个解决这些小问题，最后把答案合并起来，得到最终答案。重点讲解除法。

1. 1、加法拆分：在计算58 + 37时，可以将58拆分成50+8，可以将37拆分成30+7，计算(50 + 30) + (8 + 7)
2. 2、减法拆分（整数基准值法）：被减数－减数＝（被减数－基准值）＋（基准值－减数）。例如“632－589”，我们可以加入 600 作为基准值，则 632－589＝（632－600）＋（600－589）。
3. 3、乘法拆分：
   1. （1）24 × 3可以拆成(20 × 3) + (4 × 3)=60 + 12=72；
   2. （2）248 × 7 可以拆成(200 × 7) + (48 × 7)，48 × 7可以拆成(40 × 7) + (8 × 7)，因此最终(200 × 7) +(40 × 7) + (8 × 7)=1400 + 280+ 56 = 1736
4. 4、除法拆分：存在一个分数AB
   1. （1）把A拆成C ± D
   2. （2）分数变成两个式子加减：CB ± DB
   3. （3）注意：需要把$\frac{C}{B}$拆成简单计算的倍数关系（0.1、0.2、0.3、0.5、1、2等等）
   4. 比如：710/1600，分母是1600，而710接近800，可以拆成(800 - 90)/1600=(800/1600) - (90/1600)，第一式子是50%，第二式子约为5% ~ 6%，则答案为44% ~ 45%，通过拆分可以不用动笔计算即可得出答案。

INFO

例: 6423/4414=?

A.1.36 B.1.46 C.1.56 D.1.66

解析

先取有效数字（2~3位），我们取三位，式子变为$\frac{642}{441}$，那么我们可以把分母看成441，把分子提出个441，则变成$\frac{441+201}{441}=1+\frac{201}{441}$，$\frac{201}{441}$可以看出商不到5，大概$4^{+}$，所以答案为${1.4}^{+}$，选B

四、高位叠加

1. 高位叠加是一种简化多位数加法的速算方法，通过从高位到低位依次相加（从前往后加），逐步记录部分和并处理进位，最终完成整体计算。这种方法通过分步操作减少记忆负担，尤其适用于资料分析中需快速计算多位数总和或比例的题目。

2. 1、步骤：

   1. （1）以高位(如千位、百位)为起点，逐位相加到低位。
   2. （2）每一步相加后需记录当前位的数值，若结果超过9，需向高位进位。
   3. （3）确保每一位对齐，依次处理所有位数，最终组合部分和得出结果。

3. 2、高位叠加的优势：

   1. （1）分步计算，仅需关注当前位及进位，避免一次性处理多位数。
   2. （2）可与截位法、估算法等配合使用。例如，在选项差异较大时，先通过高位叠加快速估算，再用尾数法验证。

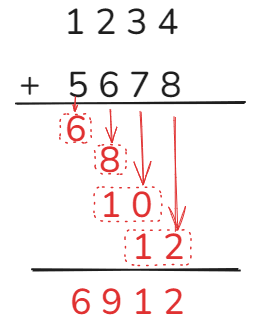
INFO

例: 1234 + 5678 = ？

解析

最终结果6912。

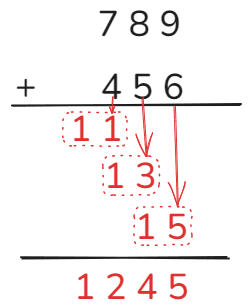
INFO

例: 789 + 456 = ？

解析

最终结果1245

五、尾数法

1. 1、原理： 在多个数字精确求和或求差时，从“尾数”处入手，为保证精确与速度，一般可观察两位（当四个选项最后一位都不一样时可只观察一位）
2. 2、题型：较多数字的精确计算 （例：相加总和题）
3. 3、步骤：
4. （1）从末尾开始计算，注意在减法中，当不够减时，要先借位，再相减。
   （2）对比选项尾数

INFO

例: 某专业有若干学生，现开设有甲、乙、丙三门选修课。有40人选修甲课程，36人选修乙课程，30人选修丙课程，兼选甲乙课程的有28人，兼选甲丙两门课程有26人，兼选乙丙两门课程的有24，三门均选的是有20人，三门均未选的有2人。该专业共有多少学生?

A.48 B.50 C.52 D.54

解析

根据容斥问题的公式可列式：40+36+30-28-26-24+20+2=总人数，利用尾数法：6+2-(8+6+4)=8-8=0，答案选B。

INFO

例: 经初步核算，2009 年上半年我国国内生产总值同比增长 7.1%，比一季度加快1.0 个百分点。其中，第一产业增加值 12025 亿元，增长 3.8%;第二产业增加值 70070 亿元，增长 6.6%;第三产业增加值 57767 亿元，增长 8.3%。 问：2009年上半年，我国国内生产总值为：

A.139862 亿元
B.147953 亿元
C.148632 亿元
D.151429 亿元

解析

根据国内生产总值的定义可知，国内生产总值等于三大产业增加值的和相加，因此 2009 年上半年国内生产总值为 12025+70070+57767。
观察选项发现后两位数据完全不同，可以利用尾数法，判断后两位尾数的和从而找出答案，尾数相加为 25+70+67=1[62]，故选 A 选项。

六、削峰填谷

• 1、定义：所谓 “削峰填谷” 指的就是将峰值的部分削掉补到不足的部分去，如果刚好能够填平就能得到一个数列的均值。这种方法往往应用在计算多个数的平均数当中
• 2、题型：较多的数字求平均数
• 3、技巧：
  • （1）给出柱状图/折线图，结合选项做基准线（画一条线），上下平衡（上线的点一样）为正确答案
  • （2）较多的数字求平均数，找基准数，算差值，计算基准 + 差值平均值
  • 比如：185，166，195，189，190求平均数，这五个数字均在180附近，将180作为平均数的基准数，这五个数字可以写成180+5；180-14；180+15；180+9；180+10；计算基准 + 差值平均值，即$180+\frac{5-4+15+9+10}{5}=185$

INFO

例: 求以下七个数字的平均数：5641、5642、5643、5641、5643、5638、5639

A. 5638~5643之间
B. 5643~5649之间

解析

这五个数字均在5640附近，将5640作为平均数的基准数，我们削峰填谷找到真实平均数与5640的距离，然后再后面依次补上超出或不足的部分。即：(3+1+3)÷7+5640=5641。选A

INFO

例:

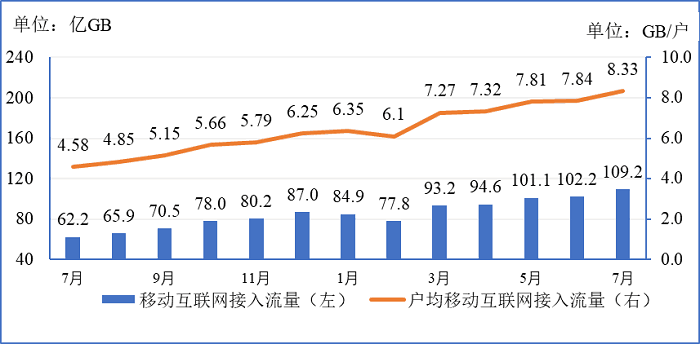
2018-2019年移动互联网接入月流量及户均流量(DOU)比较

根据上述资料，下列说法正确的是( ) A. 2018年下半年，我国移动互联网接入流量累计超过400亿GB

A. 5638~5643之间
B. 5643~5649之间

解析

定位柱状图，2018年下半年即7~12月数据，要确定我国移动互联网接入流量累计是否超过400亿，加和计算数据较多。
换种思路如果总和超过400，则6个月平均数需要超过66.6亿，根据数据，2018年下半年的六个月中，超过66.6的有4个，不足66.6的有两个。
将不足部分补齐且有剩余，因此平均数一定超过66.6，总数一定超过400亿，A选项正确。

七、分母小化分

所谓“分小互化法”就是把分数和小数的相互转换，从而提高做题速度，达到节省时间的目的。比如说，看到166的时候，可以转化为用1/6去计算，在这里需要熟练记忆相关的数字的转化。

1. 1、存在一个百分数可以化简成1/n，则基期=现期×n/(n+1)，增长量=现期/(n+1)，减少量=现期/(n-1)

1/2=0.5	1/3=0.33	1/4=0.25	1/5=0.2
1/6=0.167	1/7=0.143	1/8=0.125	1/9=0.111
1/10=0.1	1/11=0.091	1/12=0.083	1/13=0.077
1/14=0.071	1/15=0.066	1/16=0.063	1/17=0.059
1/18=0.056	1/19=0.053	1/20=0.05

INFO

例: 现期1569.7，增长率16.3%，求增长量约为（）

A.203.1 B.221.1 C.243.8 D.270.13

解析

选项误差在10%左右，可用小分互换，16.3接近16.7，把$\frac{1}{6}$带入公式增长量=$\frac{\mathrm{现}\mathrm{期}}{1+\mathrm{增}\mathrm{长}\mathrm{率}}$ × 增长率，则增长量=$\frac{1569.7}{7}$≈224，与B选项接近，选B

八、中间值法

中间值法适用于当你对答案有了一个估算的值，但无法确定二选一该选哪一个，且这两个选项分布在一个比较规整的数两侧。

• 1、 假如你的答案是一个分数$\frac{A}{B}$，选项剩余两个选项分别是a%和b%（a%<b%），此时我们就可以用B × 两个选项的中间值$\frac{a\mathrm{\%}+b\mathrm{\%}}{2}$（用R表示） 大概估一下，再和A比谁大谁小。
  • （1）如果B × R > A，说明B × R 应该乘以一个小于 R 才能得到A，此时答案应该选偏中间值小的(a%)。
  • （2）如果B × R < A，说明B × R 应该乘以一个大于 R 才能得到A，此时答案应该选偏中间值大的(b%)。

INFO

例: 2006年，全国农村从业人员数量为47852万人，其中6986万人从事第三产业;东北地区农村从业人员数量为3230万人，其中391万人从事第三产业。请问，全国、东北地区农村从业人员中从事第三产业人员的比例分别是多少?( )
A.13.6%，12.7%
B.14.6%，12.7%
C.13.6%，12.1%
D.14.6%，12.1%

解析

根据题干信息，可列出两个等式：全国=$\frac{6986}{47852}$，东北=$\frac{391}{3230}$。
观察选项可知，6986/47852，结果要么是13.6%，要么是14.6%，二者中间有个14.3%，即1/7，所以我们先看看47852的1/7是多少，47852/7明显小于7000，但是6986极其接近7000，所以6986/47852肯定大于14.3%，故全国的比例应为14.6%。
东北地区农村：391/3230，结果要么是12.7%，要么是12.1%，二者之间有个12.5%，即1/8，所以我们先看看3230的1/8是多少，明显超过400，所以391/3230比12.5%小，所以只能是12.1%。

九、差分法（分数比较）

1. 1、定义：两个分数和$\frac{a}{b}$和$\frac{c}{d}$,如果a>c,b>d，ab记为“大分数”，$\frac{c}{d}$记为“小分数”，$\frac{a-c}{b-d}$记为“差分数” 2. （1）若$\frac{a-c}{b-d}$=$\frac{c}{d}$，则$\frac{a}{b}$=$\frac{c}{d}$ 3. （2）若$\frac{a-c}{b-d}$>$\frac{c}{d}$，则$\frac{a}{b}$>$\frac{c}{d}$ 4. （3）若$\frac{a-c}{b-d}$<$\frac{c}{d}$，则$\frac{a}{b}$<$\frac{c}{d}$

2. 2、使用方法：

   • （1）分子分母都比另一个大
   • （2）用大的分子/分母减去小的分子/分母得到差分数
   • （3）然后用差分数代替大的与小的比较

3. 3、原理：类比混合溶液问题。浓度=溶质/溶液

   4. 假设一份溶液浓度为$\frac{a}{b}$，另外一份浓度为$\frac{△a}{△b}$(设为差分数)，则混合后的浓度为$\frac{a+△a}{b+△b}$

   5. 由于我们不知道$\frac{△a}{△b}$和$\frac{a}{b}$的大小，只能判断出混合的一定在两个溶液浓度之间。

   6. 如果$\frac{△a}{△b}$>$\frac{a}{b}$，可以推出：$\frac{a+△a}{b+△b}$>$\frac{a}{b}$；则线段表示为：

   7. a/b  (a+△a)/(b+△b)  △a/△b  |     |      | ------------------------------

   8. 如果$\frac{△a}{△b}$<$\frac{a}{b}$，可以推出：$\frac{a+△a}{b+△b}$>$\frac{a}{b}$<$\frac{a}{b}$；则线段表示为：

   9. △a/△b  (a+△a)/(b+△b)  a/b  |      |      | --------------------------------

INFO

例:  9/11 和 5/6 比较大小 解析 $\frac{9}{11}$为'大分数'，$\frac{5}{6}$为'小分数',$\frac{9-5}{11-6}$=$\frac{4}{5}$记为'差分数' 可以看出差分数是小于小分数的，所以大分数<小分数。所以$\frac{9}{11}$<$\frac{5}{6}$

十、拆分法（分数比较）

1、当分母大于分子，两个分数分母同时减去分子，不改变原式大小关系2、当分子大于分母，两个分数分子同时减去分母，不改变原式大小关系3、总结：谁大谁减

十一、增长率法（分数比较）

十二、错位加减法

原理：分子分母同时扩大或者缩小相同倍数或比例，分数值不变

十三、化除为乘（求基期量）

1、应用条件：

- （1）选项差距小，差距大的直接直除。
- （2）$|r|<5\%$

2.应用方法：

• （1）$\frac{A}{1+r}$≈ A ×(1-r)
• （2）$\frac{A}{1-r}$≈ A × (1+r)

应用延申：当|r|<10%，选项第二位不同也可以使用。此时误差范围<1%。

十四、415份法

1. 1、定义：415份数法与数量中的比例法类似，均是将数量关系转化为份数比例关系，从而化简计算。一般来讲，在现期A和増长率r是已知量的前提下，我们可以用415份数法求得基期B、变化量X的数值。 2. （1）415份数法中“415”分别代表基期、变化量、现期的份数，一般来说，我们只需根据增长率求出现期对应的份数，即可根据现期量求得一份的大小，再根据问题进行下一步计算。 3. （2）415份数法使用的核心公式为X=Br[增长量=基期×增长率]和B=A-X[基期=现期-变化量]。
2. 2、使用步骤： 5. （1）把增长率r换成对应的分数，化成相近的分数a/b； 6. （2）写出比例：基期、変化量、现期量之比b：a：a+b（基期为b份，变化量为a份，现期为b+a份）； 7. （3）根据现期现期量A和其对应的份数（a+b）可以求得每一份对应的量（份量）； 8. （4）根据份量的大小可求变化量、基期。
3. 3、注意： 10. （1）増长率为负数时变化量也为负数，此时“415份数法”即变成“4(-1)3份数法”。 11. （2）很多时候増长率r并不与某个分数完全相等，而是近似的看成某个分数。估算必然会产生误差，对于估算出的一份量，规则为”估大则一份变大、估小则一份变小”（把23%估算成1/4，即是估大了，则求出的一份量比实际量要大；把23%估算成1/5，即是估小了则求出的一份量比实际量要小)。如果选项中有与估算值完全一样的数据，小心有坑！！！ 12. （3）如果所求为基期，一般先求变化量，再使用公式B=A-X。不要用份量乘以基期份数，因为份量非实际值，一般是估算来的，会产生误差，用份量乘以份数则误差被扩大若干倍。
4. 3、需要经常记忆的分数：
5. 28.6%=2/7
6. 42.9%=3/7
7. 37.5%=12.5×3=3/8
8. 62.5%=5/8
9. 分母小化分

例: 2024年电子类器件平均售价785元，比去年增长28.9%，求2023年平均售价和增长量分别是多少？

解析

使用415份法，28.9%约等于28.6%=2/7，即基期：变化量：现期=7：2：9，现期为785元，所以每份为785÷9=87，增长量为87×2=174元，因此2023年平均售价为785-174=611元。

若题目是比去年增长-28.9%，则基期：变化量：现期=7：-2：5，所以每份为785÷5=157元，增长量=157×-2=-314元。因此2023年平均售价为785-（-314）=1099元。

十五、假设分配法

假设分配的核心是“抓住主要矛盾”，将“大数”分完，“小数”有误差也不影响结果。

1. 1、使用场景：求任何基期(B)和变化量(X)的题目
2. 2、使用时机: 增长率不在任何分数附近时或当求基期或变化量只是计算过程的中间步骤时。
3. 3、核心公式：变化量（X）＝基期量（B）×增长率（r），在r较小的情况下，可以用现期代替基期，X=B×r≈A×r。假设分配法通俗地说呢，就是利用核心公式一步步地把A分成B和X两个部分。
4. 4、使用步骤：
   1. （1）根据现期和增长率，假设基期量A为一个方便计算的整数；
   2. （2）根据X=B×r可计算变化量；
   3. （3）根据现期-（基期+变化量）=剩余分配量，重复步骤，直到把现期分配完即可；
   4. （4）最后把每一步分配的基期和变化量进行相加。
5. 4、注意：增长率为负或选项差距极小，不十分适用；

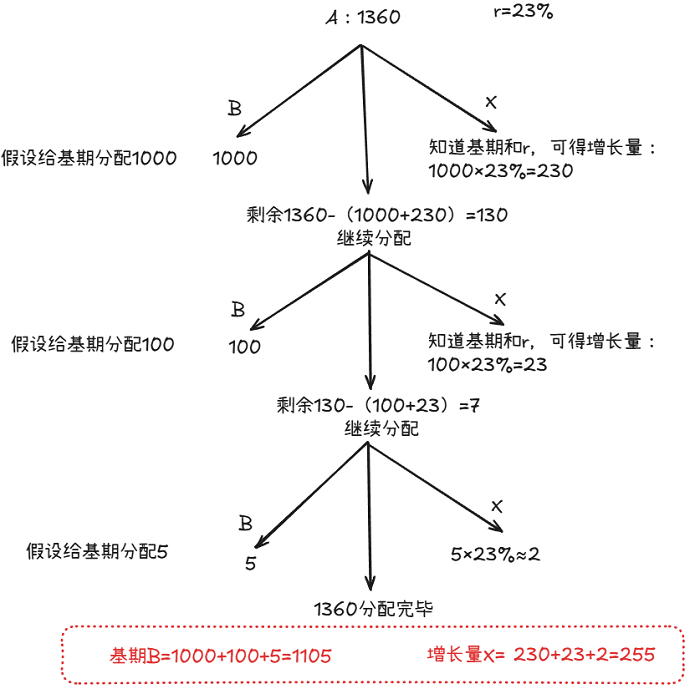
例: 现期A=1360，增长率r=23%，请求出前期B和变化量X。

解析

:

若取B=6，X=1时，r=1/6=16.7%<23%
若取B=5，X=2时，r=2/5=40%>23%
则1 < X < 2；那就取中，B=5.5，X=1.5

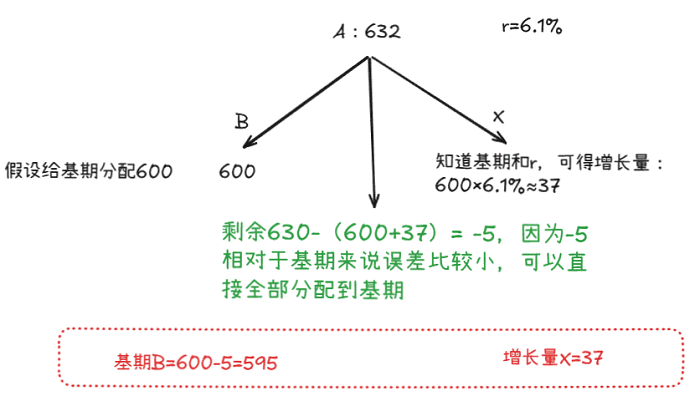
例: 现期A=632，增长率r=6.1%，请求出前期B和变化量X。

解析

画出分配树:

当然你也可以继续分配，因为r比较小（X＝Br≈Ar），先分配X为-5×6.1%≈-0.3，这里为什么X估小一点，因为在第一步X=37时就估大了，为了精确，因此第二步可以估小一点。此时B就等于-5+0.3=-4.7，那么此时B=600+(-4.7)=595.3，x=36.7。

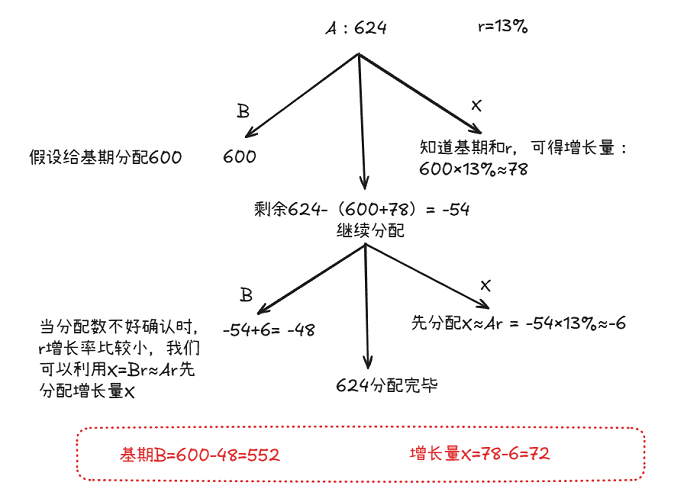
例: 现期A=624，增长率r=13%，请求出前期B和变化量X。

解析

画出分配树:

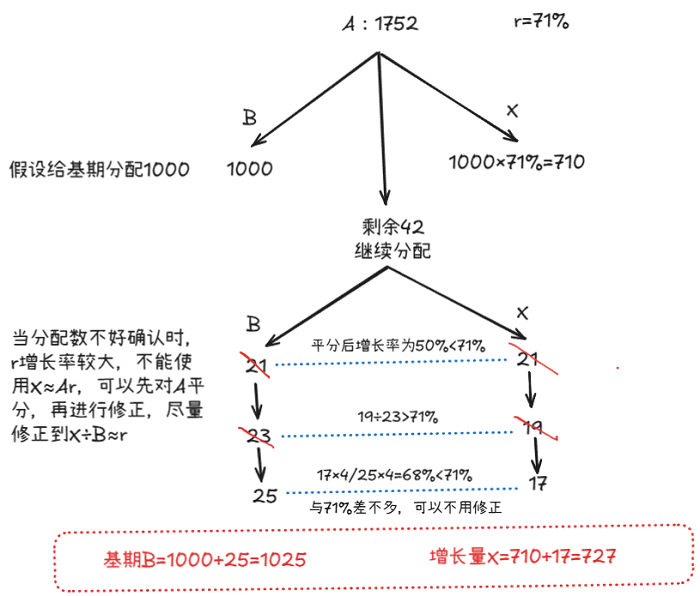
例: 现期A=1752，增长率r=71%，请求出前期B和变化量X。

解析

第一步：确定分配数1000:710，剩余42
第二步：，21：21，再进行修正，变成23：19，19/23>71%，继续修正，变成25:17，17×4/25×4等于68%，与71%差不多了。
你可以继续修正，比如变成24.5:16.5，此时就不用计算了，大概与71%相等了
因此B=1000+24.5=1024.5，X=710+16.5=726.5

总结

当r在20%以下，先确定分配数，后续在确定是否使用X≈Ar 当r在25%左右，B：X=4：1 当r在33%左右，B：X=3：1 当r在50%左右，B：X=2：1 当r在66%左右，B：X=3：2 当r在70%以上，直接平分再进行修正